崇明区第一学期教学水平调查测试题
初三数学
(考试时间:
100分钟,满分150分)
考生注意:
本试题含三个大题,共25题;
考生务必按答卷需要在答卷纸规定的地方上作答,在草稿纸上答卷一律无效;
除1、二大题外,其余各题如无特不要说明,都需要在答卷纸的相应地方上写出解题的主要步骤.
1、选择题:(本大题共6题,每题4分,满分24分)
【下列各题的四个选项中,有且只有一个选项是正确的,选择正确项的代号并填涂在答卷纸的相应地方上.】
1.假如![]() ,那样
,那样![]() 的值为 …………………………………………………………( ▲ )
的值为 …………………………………………………………( ▲ )
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
2.在![]() 中,假如
中,假如![]() ,那样
,那样![]() 表示
表示![]() 的………………………………( ▲ )
的………………………………( ▲ )
正弦; 正切; 余弦; 余切.
3.已知二次函数![]() 的图像如图所示,那样a、b的符号为 …………………( ▲ )
的图像如图所示,那样a、b的符号为 …………………( ▲ )
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
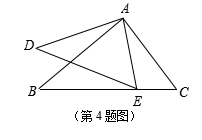
4.如图,假如![]() ,那样添加下列一个条件后,仍不可以确定
,那样添加下列一个条件后,仍不可以确定![]() 的
的
是 …………………………………………………………………………………………( ▲ )


![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
5.已知向量![]() 和
和![]() 都是单位向量,那样下列等式成立的是……………………………( ▲ )
都是单位向量,那样下列等式成立的是……………………………( ▲ )
![]() ;
; ![]() ;
; ![]() ;
; ![]() .
.
6.假如两圆的圆心距为2,其中一个圆的半径为3,另一个圆的半径![]() ,那样这两个圆的地方关系不可能是 ………………………………………………………………………( ▲ )
,那样这两个圆的地方关系不可能是 ………………………………………………………………………( ▲ )
内含; 内切; 外离; 相交.
2、填空题:(本大题共12题,每题4分,满分48分)
【请直接将结果填入答卷纸的相应地方】
7.化简:![]() __________________________________________________.
__________________________________________________.
8.已知线段b是线段a、c的比率中项,且![]() cm,
cm,![]() cm,那样
cm,那样![]() __________________________________________________cm.
__________________________________________________cm.
9.在以O为坐标原点的直角坐标平面内有一点![]() ,假如AO与y轴正半轴的夹角为
,假如AO与y轴正半轴的夹角为![]() ,
,
那样![]() __________________________________________________.
__________________________________________________.
10.假如一个正六边形的半径为2,那样这个正六边形的周长为__________________________________________________.
11.假如两个相似三角形的周长比为![]() ,那样它们的面积比为__________________________________________________.
,那样它们的面积比为__________________________________________________.
12.已知线段AB的长为10厘米,点C是线段AB的黄金分割点,且![]() ,那样线段AC的
,那样线段AC的
长为__________________________________________________厘米.
13.己知抛物线![]() ,那样这条抛物线的顶点坐标为__________________________________________________.
,那样这条抛物线的顶点坐标为__________________________________________________.
14.已知二次函数![]() ,那样它的图像在对称轴的__________________________________________________部分是降低的(填“左边”或“右边”).
,那样它的图像在对称轴的__________________________________________________部分是降低的(填“左边”或“右边”).
15.已知![]() 中,
中,![]() ,
,![]() ,
,![]() ,G为
,G为![]() 的重点,那样
的重点,那样![]() __________________________________________________.
__________________________________________________.
16.如图,正方形DEFG的边EF在![]() 的边BC上,顶点D、G分别在边AB、AC上.
的边BC上,顶点D、G分别在边AB、AC上.
已知![]() ,
,![]() 的高
的高![]() ,则正方形DEFG的边长为__________________________________________________.
,则正方形DEFG的边长为__________________________________________________.


17.已知![]() 中,
中,![]() ,
,![]() ,
,![]() .假如以点C为圆心的圆与斜边AB有唯一的公共点,那样⊙C的半径R的取值范围为__________________________________________________.
.假如以点C为圆心的圆与斜边AB有唯一的公共点,那样⊙C的半径R的取值范围为__________________________________________________.
18.假如从一个四边形一边上的点到对边的视角是直角,那样称该点为直角点.比如,如图的四边形ABCD中,点M在CD边上,连结AM、BM,![]() ,则点M为直角点.
,则点M为直角点.
若点E、F分别为矩形ABCD边AB、CD上的直角点,且![]() ,
,![]() ,则线段EF的
,则线段EF的
长为__________________________________________________.
3、解答卷:(本大题共7题,满分78分)
19.(本题满分10分)
计算:![]() .
.
20.(本题满分10分,每小题各5分)
如图,在![]() 中,点D、E分别在边AB、AC上,
中,点D、E分别在边AB、AC上,![]() ,且
,且![]() .
.
 (1)假如
(1)假如![]() ,求AE的长;
,求AE的长;
(2)设![]() ,
,![]() ,求向量
,求向量![]() (用向量
(用向量![]() 、
、![]() 表示).
表示).
21.(本题满分10分,每小题各5分)
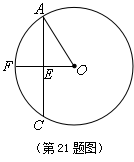 已知:如图,AO是⊙O的半径,AC为⊙O的弦,点F为
已知:如图,AO是⊙O的半径,AC为⊙O的弦,点F为![]() 的中点,OF交AC于点E,
的中点,OF交AC于点E,![]() ,
,![]() .
.
(1)求AO的长;
(2)过点C作![]() ,交AO延长线于点D,
,交AO延长线于点D,
求![]() 的值.
的值.
22.(本题满分10分,每小题各5分)
安装在屋顶的太阳能热水器的横截面示意图如图所示。已知集热管AE与支架BF所在直线相交于水箱横截面⊙O的圆心O,⊙O的半径为0.2米,AO与屋面AB的夹角为32°,与铅垂线OD的夹角为40°,![]() ,垂足为B,
,垂足为B,![]() ,垂足为D,
,垂足为D,![]() 米.
米.
(1)求支架BF的长;
 (2)求屋面AB的坡度.
(2)求屋面AB的坡度.
(参考数据:![]() ,
,![]() ,
,![]() )
)
23.(本题满分12分,每小题各6分)
如图,![]() 中,D是BC上一点,E是AC上一点,点G在BE上,联结DG并延长交AE于点F,
中,D是BC上一点,E是AC上一点,点G在BE上,联结DG并延长交AE于点F,![]() .
.
 (1)求证:
(1)求证:![]() ;
;
(2)假如![]() ,求证:
,求证:![]() .
.
24.(本题满分12分,每小题各4分)
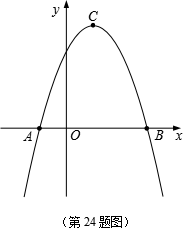
如图,在平面直角坐标系![]() 中,二次函数
中,二次函数![]() (a、b都是常数,且
(a、b都是常数,且![]() )的图像与x轴交于点
)的图像与x轴交于点![]() 、
、![]() ,顶点为点C.
,顶点为点C.
(1)求这个二次函数的分析式及点C的坐标;
(2)过点B的直线![]() 交抛物线的对称轴于点D,联结BC,求∠CBD的余切值;
交抛物线的对称轴于点D,联结BC,求∠CBD的余切值;
(3)点P为抛物线上一个动点,当![]() 时,求点P的坐标.
时,求点P的坐标.
25.(本题满分14分,其中第(1)小题4分,第(2)小题5分,第(3)小题5分)
如图,在![]() 中,
中,![]() ,
,![]() ,
,![]() ,垂足为D,点P是边AB上的一个动点,过点P作
,垂足为D,点P是边AB上的一个动点,过点P作![]() 交线段BD于点F,作PG⊥AB交AD于点E,交线段CD于点G,设
交线段BD于点F,作PG⊥AB交AD于点E,交线段CD于点G,设![]() .
.
(1)用含x的代数式表示线段DG的长;
(2)设![]() 的面积为y,求y与x之间的函数关系式,并写出概念域;
的面积为y,求y与x之间的函数关系式,并写出概念域;
(3)![]() 能否为直角三角形?
能否为直角三角形?
 假如能,求出BP的长;假如不可以,请说明理由.
假如能,求出BP的长;假如不可以,请说明理由.







